主成份(Principal Component Analysis)分析是降维(Dimension Reduction)的重要手段。每一个主成分都是数据在某一个方向上的投影,在不同的方向上这些数据方差Variance的大小由其特征值(eigenvalue)决定。一般我们会选取最大的几个特征值所在的特征向量(eigenvector),这些方向上的信息丰富,一般认为包含了更多我们所感兴趣的信息。当然,这里面有较强的假设:(1)特征根的大小决定了我们感兴趣信息的多少。即小特征根往往代表了噪声,但实际上,向小一点的特征根方向投影也有可能包括我们感兴趣的数据; (2)特征向量的方向是互相正交(orthogonal)的,这种正交性使得PCA容易受到Outlier的影响,例如在【1】中提到的例子(3)难于解释结果。例如在建立线性回归模型(Linear Regression Model)分析因变量(response)和第一个主成份的关系时,我们得到的回归系数(Coefficiency)不是某一个自变量(covariate)的贡献,而是对所有自变量的某个线性组合(Linear Combination)的贡献。
在Kernel PCA分析之中,我们同样需要这些假设,但不同的地方是我们认为原有数据有更高的维数,我们可以在更高维的空间(Hilbert Space)中做PCA分析(即在更高维空间里,把原始数据向不同的方向投影)。这样做的优点有:对于在通常线性空间难于线性分类的数据点,我们有可能再更高维度上找到合适的高维线性分类平面。我们第二部分的例子就说明了这一点。
本文写作的动机是因为作者没有找到一篇好的文章(看了wikipedia和若干google结果后)深层次介绍PCA和Kernel PCA之间的联系,以及如何以公式形式来解释如何利用Kernel PCA来做投影,特别有些图片的例子只是展示了结果和一些公式,这里面具体的过程并没有涉及。希望这篇文章能做出较好的解答。
1. Kernel Principal Component Analysis 的矩阵基础
我们从解决这几个问题入手:传统的PCA如何做?在高维空间里的PCA应该如何做?如何用Kernel Trick在高维空间做PCA?如何在主成分方向上投影?如何Centering 高维空间的数据?
1.1 传统的PCA如何做?
让我先定义如下变量: [latex] X= [x_1, x_2, \ldots, x_N] [/latex] 是一个[latex] d \times N [/latex]矩阵,代表输入的数据有[latex] N[/latex] 个,每个sample的维数是[latex] d [/latex]。我们做降维,就是想用[latex] k [/latex]维的数据来表示原始的[latex]d[/latex]维数据([latex] k \le d [/latex])。
当我们使用centered的数据(即[latex]\sum_i x_i = 0[/latex])时,可定义协方差矩阵[latex]C[/latex]为:
[mathjax]
$$C=\frac{1}{N} x_i x_i^T = \frac{1}{N} X X^T$$
做特征值分解,我们可以得到:
$$CU = U \Lambda \Rightarrow C = U \Lambda U^T = \sum_a \lambda_a u_a u_a^T$$
注意这里的[latex]C, U , \Lambda[/latex]的维数都是[latex]d \times d[/latex], 且[latex] U=[u_1, u_2, \ldots, u_d] [/latex], [latex]\Lambda = diag(\lambda_1, \lambda_2, \ldots, \lambda_d) [/latex]。
当我们做降维时,可以利用前[latex]k[/latex]个特征向量[latex]U_k = [u_1, u_2, \ldots, u_k] [/latex]。则将一个[latex]d[/latex]维的[latex]x_i[/latex]向[latex]k[/latex]维的主成分的方向投影后的[latex]y_i = U_k^T x_i[/latex] (这里的每一个[latex]u_i[/latex]都是[latex]d[/latex]维的,代表是一个投影方向,且[latex]u_i^T u_i = 1[/latex],表示这是一个旋转变量)
1.2 在高维空间里的PCA应该如何做?
高维空间中,我们定义一个映射[latex]\Phi : X^d \rightarrow \mathcal{F}[/latex],这里[latex]\mathcal{F}[/latex]表示Hilbert泛函空间。
现在我们的输入数据是[latex]\Phi(x_i), i = 1, 2, …n[/latex], 他们的维数可以说是无穷维的(泛函空间)。
在这个新的空间中,假设协方差矩阵同样是centered,我们的协方差矩阵为:
$$\bar{C}=\frac{1}{N} \Phi(x_i) \Phi(x_i)^T = \frac{1}{N} \Phi(X) \Phi(X)^T$$
这里有一个陷阱,我跳进去过:
在对Kernel trick一知半解的时候,我们常常从形式上认为[latex]\bar{C} [/latex]可以用[latex]K_{i,j} = K(x_i, x_j)[/latex]来代替,
因此对[latex]K=(K_{ij})[/latex]做特征值分解,然后得到[latex]K=U \Lambda U^T[/latex],并且对原有数据降维的时候,定义[latex]Y_i=U_k^T X_i[/latex]。
但这个错误的方法有两个问题:一是我们不知道矩阵[latex]\bar{C}[/latex]的维数;二是[latex]U_k^T X_i[/latex]从形式上看不出是从高维空间的[latex]\Phi(X_i)[/latex]投影,并且当有新的数据时,我们无法从理论上理解[latex] U_k^T X_{\mathrm{new}} [/latex]是从高维空间的投影。
如果应用这种错误的方法,我们有可能得到看起来差不多正确的结果,但本质上这是错误的。
正确的方法是通过Kernel trick将PCA投影的过程通过内积的形式表达出来,详细见1.3
1.3 如何用Kernel Trick在高维空间做PCA?
在1.1节中,通过PCA,我们得到了[latex]U[/latex]矩阵。这里将介绍如何仅利用内积的概念来计算传统的PCA。
首先我们证明[latex]U[/latex]可以由[latex]x_1, x_2, \ldots, x_N[/latex]展开(span):
$$ C u_a = \lambda_a u_a $$
$$ \begin{align}
u_a &= \frac{1}{\lambda_a} C u \\
&= \frac{1}{\lambda_a} (\sum_i x_i x_i^T )u \\
&= \frac{1}{\lambda_a} \sum_i x_i (x_i^T u) \\
&= \frac{1}{\lambda_a} \sum_i (x_i^T u) x_i \\
&= \sum_i \frac{x_i^T u}{\lambda_a} x_i \\
&= \sum_i \alpha_i^a x_i
\end{align}$$
这里定义[latex]\alpha_i^a=\frac{x_i^T u}{\lambda_a} [/latex]。
因为[latex]x_i^T u[/latex] 是一个标量(scala),所以[latex]\alpha_i^a[/latex]也是一个标量,因此[latex]u_i[/latex] 是可以由[latex]x_i[/latex]张成。
进而我们显示PCA投影可以用内积运算表示,例如我们把[latex]x_i[/latex]向任意一个主成分分量[latex]u_a[/latex]进行投影,得到的是[latex]u_a^T x_i[/latex],也就是[latex]x_i^T u_a[/latex] 。作者猜测写成这种形式是为了能抽出[latex]x_i^T x_j = \mathrm{<} x_i, x_j\mathrm{>} [/latex]的内积形式。
$$\begin{align}
x_i^T C u_a &= \lambda_a x_i^T u_a \\
x_i^T \frac{1}{N} \sum_j x_j x_j^T \sum_k \alpha_k^a x_k &= \lambda_a x_i^T \sum_k \alpha_k^a x_k \\
\sum_j \alpha_k^a \sum_k (x_i^T x_j) (x_j^T x_k) &= N \lambda_a \sum_k \alpha_k^a (x_i^T x_k) \\
\end{align}$$
当我们定义[latex] K_{ij} = x_i^T x_j [/latex]时,上式可以写为[latex] K^2 \alpha = N \lambda_a K \alpha^a[/latex]
(这里[latex]\alpha^a[/latex]定义为[latex][\alpha_1^a, \alpha_2^a, \ldots, \alpha_N^a]^T[/latex].)
进一步,我们得到解为:
$$K \alpha = \tilde{\lambda}_a \alpha \quad \mathrm{with} \quad \tilde{\lambda}_a = N \lambda_a$$
[latex]K[/latex]矩阵包含特征值[latex]\tilde{\lambda}[/latex]和[latex]\alpha^a[/latex],我们可以通过[latex]\alpha[/latex]可以计算得到[latex]u_a[/latex],
注意特征值分解时Eigendecomposition,[latex]\alpha^a[/latex]只代表一个方向,它的长度一般为1,但在此处不为1。
这里计算出[latex]\alpha_a[/latex]的长度(下面将要用到):
因为[latex]u_a[/latex]的长度是1,我们有:
$$\begin{align}
1 &= u_a^T u_a \\
&= ( \sum_i \alpha_i^a x_i) ^T (\sum_j \alpha_j^a x_j ) \\
&= \sum_i \sum_j \alpha_i^a \alpha_j^a x_i^T x_j^T \\
&=(\alpha^a)^T K \alpha_a \\
&=(\alpha^a)^T ( N \lambda_a \alpha_a) \\
&=N \lambda_a ({\alpha^a}^T \alpha_a )\\
&\Rightarrow \quad \lVert \alpha^a \rVert = 1/\sqrt{N \lambda_a} = 1/\sqrt{\tilde{\lambda}_a}
\end{align}$$
在上面的分析过程中,我们只使用了内积。因此当我们把[latex]K_{ij} = x_i^T x_j[/latex]推广为[latex]K_{ij} = <\Phi(x_i), \Phi(x_j> = \Phi(x_i)^T \Phi(x_j)[/latex]时,上面的分析结果并不会改变。
1.4 如何在主成分方向上投影?
投影时,只需要使用[latex]U[/latex]矩阵,假设我们得到的新数据为[latex]t[/latex],那么[latex]t[/latex]在[latex]u_a[/latex]方向的投影是:
$$u_a^T t = \sum_i \alpha_i^a x_i^T t = \sum_i \alpha_i^a ( x_i^T t)$$
对于高维空间的数据[latex]\Phi(x_i),\Phi(t)[/latex],我们可以用Kernel trick,用[latex]K(x_i, t)[/latex]来带入上式:
$$u_a^T t = \sum_i \alpha_i^a K(x_i, t)$$
1.5 如何Centering 高维空间的数据?
在我们的分析中,协方差矩阵的定义需要centered data。在高维空间中,显式的将[latex]\Phi(x_i)[/latex]居中并不简单,
因为我们并不知道[latex]\Phi[/latex]的显示表达。但从上面两节可以看出,所有的计算只和[latex]K[/latex]矩阵有关。具体计算如下:
令[latex]\Phi_i = \Phi(x_i)[/latex],居中[latex]\Phi_i^C = \Phi_i – \frac{1}{N}\sum_k \Phi_k[/latex]
$$\begin{align}
K_{ij}^C
&= <\Phi_i^C \Phi_j^C> \\
&= (\Phi_i – \frac{1}{N}\sum_k \Phi_k)^T (\Phi_j – \frac{1}{N}\sum_l \Phi_l ) \\
&=\Phi_i^T\Phi_j – \frac{1}{N}\sum_l \Phi_i^T \Phi_l – \frac{1}{N}\sum_k \Phi_k^T \Phi_j + \frac{1}{N^2}\sum_k \sum_l \Phi_k^T \Phi_l \\
&=K_{ij} – \frac{1}{N}\sum_l K_{il} – \frac{1}{N}\sum_k K_{kj} + \frac{1}{N^2}\sum_k \sum_l K_{kl}
\end{align}$$
不难看出,
$$K^C = K – 1_N K – K 1_N + 1_N K 1_N$$
其中[latex]1_N[/latex] 为[latex]N \times N [/latex]的矩阵,其中每一个元素都是[latex]1/N[/latex]
对于新的数据,我们同样可以
$$\begin{align}
K(x_i, t)^C
&= <\Phi_i^C \Phi_t^C> \\
&= (\Phi_i – \frac{1}{N}\sum_k \Phi_k)^T (\Phi_t – \frac{1}{N}\sum_l \Phi_l ) \\
&=\Phi_i^T\Phi_t – \frac{1}{N}\sum_l \Phi_i^T \Phi_l – \frac{1}{N}\sum_k \Phi_k^T \Phi_t + \frac{1}{N^2}\sum_k \sum_l \Phi_k^T \Phi_l \\
&=K(x_i,t) – \frac{1}{N}\sum_l K_{il} – \frac{1}{N}\sum_k K(x_k,t) + \frac{1}{N^2}\sum_k \sum_l K_{kl}
\end{align}$$
2. 演示 (R code)
首先我们应该注意输入数据的格式,一般在统计中,我们要求[latex]X[/latex]矩阵是[latex]N \times d[/latex]的,但在我们的推导中,[latex]X[/latex]矩阵是[latex]d \times N[/latex]。
这与统计上的概念并不矛盾:在前面的定义下协方差矩阵为[latex]X^T X[/latex],而在后面的定义中是[latex]X X^T[/latex]。另外这里的协方差矩阵是样本(Sample)的协方差矩阵,我们的认为大写的X代表矩阵,而不是代表一个随机变量。
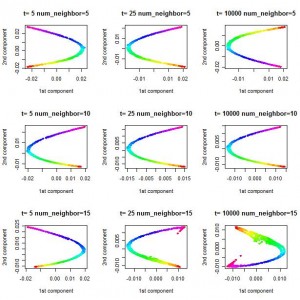
另外,在下面的结果中,Gaussian 核函数(kernel function)的标准差(sd)为2。在其他取值条件下,所得到的图像是不同的。
KPCA图片:

R 源代码(Source Code):链接到完整的代码 KernelPCA
Kernel PCA部分代码:
# Kernel PCA
# Polynomial Kernel
# k(x,y) = t(x) %*% y + 1
k1 = function (x,y) { (x[1] * y[1] + x[2] * y[2] + 1)^2 }
K = matrix(0, ncol = N_total, nrow = N_total)
for (i in 1:N_total) {
for (j in 1:N_total) {
K[i,j] = k1(X[i,], X[j,])
}}
ones = 1/N_total* matrix(1, N_total, N_total)
K_norm = K - ones %*% K - K %*% ones + ones %*% K %*% ones
res = eigen(K_norm)
V = res$vectors
D = diag(res$values)
rank = 0
for (i in 1:N_total) {
if (D[i,i] < 1e-6) { break }
V[,i] = V[,i] / sqrt (D[i,i])
rank = rank + 1
}
Y = K_norm %*% V[,1:rank]
plot(Y[,1], Y[,2], col = rainbow(3)[label], main = "Kernel PCA (Poly)"
, xlab="First component", ylab="Second component")
3. 主要参考资料
【1】A Tutorial on Principal Component Analysis ,Jonathon Shlens�, Shlens03
【2】Wikipedia: http://en.wikipedia.org/wiki/Kernel_principal_component_analysis
【3】 Original KPCA Paper:Kernel principal component analysis,Bernhard Schölkopf, Alexander Smola and Klaus-Robert Müller http://www.springerlink.com/content/w0t1756772h41872/fulltext.pdf
【4】Max Wellings’s classes notes for machine learning Kernel Principal Component Analaysis http://www.ics.uci.edu/~welling/classnotes/papers_class/Kernel-PCA.pdf