拉格朗日乘数检验
Lagrange Multiplier test (Score test)
拉格朗日乘数检验，英文是Lagrange multiplier test，或者叫做Score test是一种常用的统计检验。
拉格朗日乘数检验的名称来源于这个检验用的是拉格朗日乘数的分布，见［2］。
Score test的名称则来自于Score本身。
为了写起来方便，下面都用Score Test来代替拉格朗日乘数检验。
Score Test，Likelihood Ratio Test和Wald Test的图形表示
假设似然函数\( L(.) \) 只有一个参数, 这三种检验可以在一张图里表示出来：
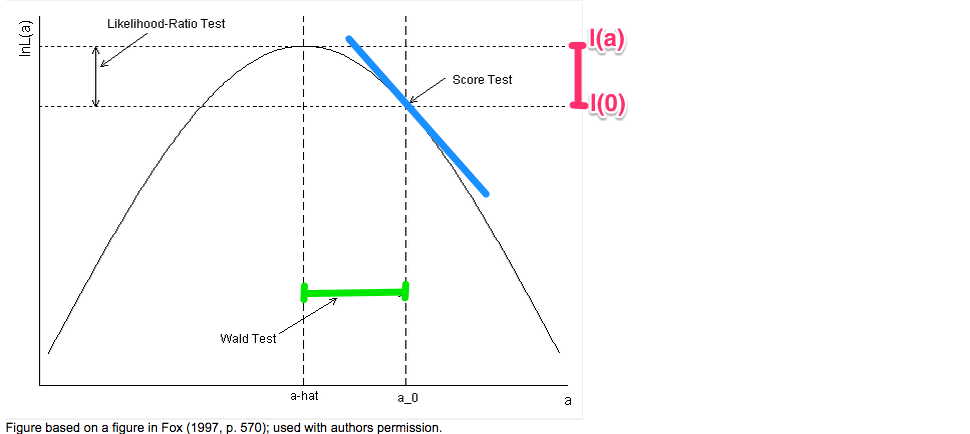
（摘自：http://www.ats.ucla.edu/stat/mult_pkg/faq/general/nested_tests.htm）
Likelihood Ratio Test计算的是\( \xi^R = 2 (l(\hat{a}) – l(0)) \), 就是两倍红色竖线的长度，这个统计量近似有自由度为1的卡方分布（假设只有一个自由变量）
这里的\(\hat{a}\)是最大似然估计（Maximum Likelihood Estimator):
$$
\xi^R = 2 (l(\hat{a}) – l(0)) = 2 log(L(\hat{a})/L(0)) \sim \chi^2_1
$$
Score Test只需要考虑\( 0 \) 这一点上似然函数的性质，在图像上通过蓝色部分表示（通过考察这一点的斜率和曲率）。
写成公式是：
$$
\begin{align}
斜率 &＝ U = l'(0) \\
|曲率| &＝ V = |l”(0)| = -l”(0) \\
\xi^S &= U’ * V^{-1} * U = \frac{l'(0)^2}{|l”(0)|} \sim \chi^2_1
\end{align}
$$
而Wald Test只需要考虑\(\hat{a}\)这一点上似然函数的性质，在图像上用绿色的横线表示的（通过比较绿色横线的宽度和在\(\hat{a}\)的曲率）。
$$
\begin{align}
斜率 &＝ l'(a) \\
\xi^W &= \hat{a}^2 * |l”(a)| \sim \chi^2_1
\end{align}
$$
Score Test等价于Likelihood Ratio Test和Wald Test
从渐进性质（Asymptotic property）上讲，Score Test和Likelihood Ratio Test（LRT），Wald Test是等价的。
详细的严格的证明可以参见［2］，文献里有更一般的结论（不限于自由度等于一）。
但是在不严格的意思下，我们可以用一个简化的例子来展示这种等价性质。
仍然假定\( H0: a = 0 \) 以及 \( H_a: a \neq 0 \)。
对于Likelihood Ratio Test （LRT），统计量（test statistics）是两倍红线的长度：
$$
\chi^{R} = 2 * ( l(\hat{a}) – l(0))
$$
首先证明Wald Test和LRT是等价的。
$$
l(0) = l(\hat{a}) – \hat{a} l'(\hat{a}) + \frac{1}{2} \hat{a}^2 l”(\hat{a})
$$
根据MLE的性质，\(l'(\hat{a}) = 0 \)。因此：
$$
l(0) = l(\hat{a}) + \frac{1}{2} \hat{a}^2 l”(\hat{a})
$$
整理一下，得到：
$$
\xi^R = 2 (l(\hat{a}) – l(0)) = \hat{a}^2 * (-l”(\hat{a})) = \hat{a}^2 * |l”(\hat{a})|= \xi^W
$$
接下来证明Score Test和LRT是等价的。
根据泰勒展开和MLE的性质：
$$
\begin{align}
l(\hat{a}) &= l(0) + \hat{a} * l'(0) + \frac{1}{2}\hat{a}^2 * l”(0) \\
l'(\hat{a}) &= l'(0) + \hat{a} * l”(0) = 0
\end{align}
$$
第二行的式子可以写成：
$$
\hat{a} = – \frac{l'(0)}{l”(0)}
$$
第一行可以写成：
$$
\begin{align}
\xi^R &= 2* (l(\hat{a}) – l(0)) = 2 * \hat{a} * l'(0) + \hat{a}^2 * l”(0) \\
&= – 2 * \frac{l'(0)^2}{l”(0)} + \frac{l'(0)^2}{l”(0)} \\
&= \frac{l'(0)^2}{-l”(0)} \\
&= \frac{l'(0)^2}{|l”(0)|} \\
&= \xi^S
\end{align}
$$
在上面的推导中，我们用到了多次\(l”()\)，这个函数一般是负数。对这个函数取期望就是Fisher Information。
而Fisher Information的倒数或者是逆矩阵，就是Score statistics的方差。
Score Test的形式
上面的例子都是检验一个参数，如果参数个数多于一，那么有更一般的结论。
假设参数是\(\theta = (\theta_1, \theta_2) \)，这里\(\theta_1,\theta_2\)分别是长度为\(p_1,p_2\)的向量，
假设检验的是： \(H_0: \theta_1 = 0, H_a: \theta_1 \neq 0\).
首先计算\(H_0\)下的MLE,假设是： \(\hat{\theta} = (0, \hat{\theta}_2) \)。然后计算U和V
$$
\begin{align}
U &= Score = l'(\hat{\theta}) = l'( (\theta_1 = 0, \hat{\theta}_2) ) \\
V &= I^{11}_{\hat{\theta}} = (I_{11} – I_{12} (I_{22})^{-1} I_{22} )_{\hat{\theta}}
\end{align}
$$
这里\(I\)是Fisher information：
$$
I(\theta)
= \left[ \begin{array}{cc}
I_{11} & I_{12} \\
I_{21} & I_{22}
\end{array} \right]_\theta
= \left[ \begin{array}{cc}
I_{11}(\theta) & I_{12}(\theta) \\
I_{21}(\theta) & I_{22}(\theta)
\end{array} \right]
$$
最后，统计量\( U * V^{-1} * U’ \sim \chi_{p_1} \)。
为什么上面的\(V\)不是\(I_{11}(\theta)\)，而是\(I_{11}(\theta)\)减去额外的一项呢？
可以认为检验\(\theta_1\) 实际上是在控制\(\theta_2\)的同时检验\(\theta_1\)，
因此\(\theta_1\)是在\(\theta_2\)的residual space里面，因此它本身的变化（Variance）就小了。
举例来说（下一节的例子也会提到），假设\(H_0: b = 0, H_a: b \neq 0\)。
如果模型是\( Y = X b + \epsilon, \epsilon_{ii} \sim N(0,1) \)。
那么\( V = \sigma^2 (X’X) \).
如果模型是\( Y = X b + Z r + \epsilon, \epsilon_{ii} \sim N(0,1) \)，
那么按照公式，第一种方法的得到的\( V = X’X – X’Z (Z’Z)^{-1} Z X = V_{XX} \)
另一种方法是求出X的Residual adjusting for Z:
$$
X_Z = (I-H) X = (I – Z (Z’Z)^{-1} Z’ ) X
$$
可以得到：
$$
V_{XX} = X_Z’ X_Z = X’ (I-H)’ (I-H) X = X’ (I – H) X = X’X – X’Z(Z’Z)^{-1}ZX
$$
这和第一种方法得到的\(V\)是等价的。
上面的例子假设误差是独立同分布的，我们也可以推广到generalized linear regression。
那么相应的\(V\)项就是\(X’WX – X’W (X’W^{-1}X)^{-1} W X’\)，
其中\(W\)可以是已知的，或者通过mean function求出来的。
比如Logistic regression里\(W = \mu * (1-\mu)\)。
更一般的结论可以参考［1］。
一些例子
下面给出一些具体例子，都假设 \(H_0: \theta_1 = 0, H_a: \theta_1 \neq 0\)。
1. 简单的线性回归（Simple Linear Regression) ：\( Y = X b + \epsilon, \epsilon_{ii} \sim N(0,\sigma^2) \)
$$
l(b, \sigma^2) = – \frac{n}{2} \log(\sigma^2) – \frac{(Y-Xb)'(Y-Xb)}{2 \sigma^2}
$$
可以求出\(\hat{\sigma}^2 = \frac{1}{n} Y’Y \)
$$
U_b = \frac{\partial l}{\partial b} = Y’X / \hat{\sigma}^2 \\
V_{bb} = -\frac{\partial l^2}{\partial^2 b} = X’X / \hat{\sigma}^2\\
$$
因此\(\xi^S = \frac{(Y’X / \hat{\sigma}^2)^2}{ X’X / \hat{\sigma}^2 } = \frac{ (Y’X)^2 }{(X’X)(Y’Y)/n} \sim \chi^2_1\).
当\(X\)和\(Y\)的均值都是零的时候（centered），\(\xi^S = n r^2\).
这里\(r\)是皮尔森相关系数（Pearson correlation coefficient）。
2. 一般的线性回归：\( Y = X b + Z r + \epsilon, \epsilon_{ii} \sim N(0,1) \)
$$
\begin{align}
U_b &= \frac{\partial l}{\partial b} = (Y – Z \hat{r})’X / \hat{\sigma}^2 \\
V_{bb} &= -\frac{\partial l^2}{\partial^2 b} = (X’X – X’Z(Z’Z)^{-1}Z’X) / \hat{\sigma}^2\\
\hat{\sigma}^2 &＝ \frac{ (Y-Z \hat{r})'(Y-Z \hat{r})}{n} \\
\hat{r} &= (Z’Z)^{-1} Z’Y
\end{align}
$$
上面的形式也许不太好记，不过如果定义\(H_Z = Z(Z’Z)^{-1}Z’\)，则有：
$$
\begin{align}
U_b &= Y'(I-H_z)X \\
V_{bb} &= X'(I-H_z)X /\hat{\sigma}^2 ]\\
\hat{\sigma}^2 &＝ \frac{ Y’ (I-H_z) Y }{n} \\
\end{align}
$$
可见\( I-H_z \)在这里有关键作用，如果让:
$$
X_z = (I-H_z)X \\
Y_z = (I-H_z)Y
$$
那么上面的Score test等价于第一种情况： \( Y_z = X_z b + \epsilon, \epsilon_{ii} \sim N(0, 1)\).
此外还可以证明\(\) \xi^S < \xi^R < \xi^W [/latex]，见［2］。3. Logistic回归： [latex]logit(E(Y)) = X b [/latex]$$ \begin{align} l &= \sum_i y_i \log(p_i) + (1-y_i) * \log(1-p_i) \\ & = \sum_i y_i \log(\frac{p}{1-p}) + log(1-p_i) \\ & = Y'X b - \sum_i \log(1+\exp(X_i b)) \end{align} $$$$ \begin{align} U &= \frac{\partial l}{\partial b} = Y'X - (\frac{\exp(Xb)}{1+\exp(Xb)})' X = (Y - \hat{Y})' X \\ V &= - \frac{\partial^2 l}{\partial b^2} = - \frac{\partial -X' \hat{Y}}{\partial b} = X' \frac{\exp(Xb)}{(1+\exp(Xb))^2} X = X' W X \\ \end{align} $$ 上式中[latex]W = diag(\hat{y} * (1-\hat{y})) [/latex]. 在[latex]H_0[/latex]下，[latex]b = 0 [/latex]，因此： $$ \begin{align} U_b &= (Y - \frac{1}{2})' X \\ V_{bb} &= \frac{1}{4} X' X \\ \end{align} $$4. Logistic回归： [latex]logit(E(Y)) = X b + Z r[/latex]$$ \begin{align} l &= \sum_i y_i \log(p_i) + (1-y_i) * \log(1-p_i) \\ & = \sum_i y_i \log(\frac{p}{1-p}) + log(1-p_i) \\ & = Y'(X b + Zr) - \sum_i \log(1+\exp(X_i b + Z_i r)) \end{align} $$ 经过一些跳步： $$ \begin{align} U_b &= \frac{\partial l}{\partial b} = (Y - \hat{Y})' X \\ V_{bb} &= - \frac{\partial^2 l}{\partial b^2} = X' W X － X'WZ (Z'WZ)^{-1} Z'W X \\ \hat{Y} &= \frac{1}{1 + \exp(- Z \hat{r} )} \end{align} $$ 类似的，上式中[latex]W = diag(\hat{y} * (1-\hat{y})) [/latex]. [latex]\hat{r}[/latex]是在[latex]b=0[/latex]时的MLE估计。 上面这个形式和［3］里的公式是等价的。[1] Chen, C.-F. Score Tests for Regression Models. Journal of the American Statistical Association (1983).doi:10.1080/01621459.1983.10477945 [2] Lin, D.-Y. & Tang, Z.-Z. A General Framework for Detecting Disease Associations with Rare Variants in Sequencing Studies. Am. J. Hum. Genet. 89, 354–67 (2011). [3] Liu, D. et al. Meta-analysis of gene-level tests for rare variant association. Nature Genetics 46, 200204 (2013).