拉普拉斯方法(Laplace’s Method)
[mathjax]
拉普拉斯方法又称为拉普拉斯近似（Laplace Approximation）。它可以用来计算一元或多元积分［1］。
举例来说，假设 $latex f(x)$ 是一维函数，我们要计算
[latex] \int_{-\infty}^{\infty} f(x) \mathrm{d} x [/latex].
如果$latex f(x)$形式很复杂，我们往往找不到定积分的公式（Close form）。
如果用数值方法来计算积分，计算量又很大。
所以要想个办法，得到一个比较精确的积分结果。
拉普拉斯方法可以适用于这种情况。我们先用泰勒展开（Taylor Expansion）：
$$ f(x) \approx f(x_0) + f'(x_0)(x-x_0) + \frac{1}{2}f”(x_0) (x-x_0)^2 $$
如果选取$latex x_0$使得$latex f'(x_0) = 0$，则可以进一步简化为
$$ f(x) \approx f(x_0) + \frac{1}{2}f”(x_0) (x-x_0)^2 $$
再引入一个假设，$latex \int_{-\infty}^{\infty} f(x) \mathrm{d} x $
可以被写成 $latex \int_{-\infty}^{\infty} e^{f(x)} \mathrm{d} x $ 的形式，那么就有：
$$ \begin{align}
\int_{-\infty}^{\infty} e^{f(x)} \mathrm{d} x
&\approx \int_{-\infty}^{\infty} e^{f(x_0) + \frac{1}{2}f”(x_0) (x-x_0)^2} \mathrm{d} x \\
&= e^{f(x_0)} \int_{-\infty}^{\infty} e^{- \frac{1}{2}|f”(x_0)| (x-x_0)^2} \mathrm{d} x \\
&= e^{f(x_0)} \sqrt{\frac{2\pi}{|f”(x_0)|}}
\end{align}
$$
注意上式中$latex f”(x_0)$要取绝对值。因为$latex f'(x_0) = 0$，$latex x_0$是$latex f(x)$的极值点。
对于概率密度函数而言，一般它也是最大值点（mode）， 因此$latex f”(x_0) < 0$.
从几何上讲，拉普拉斯方法是要用一个$latex e^{-x^2}$形式的函数近似$latex f(x)$.
或者说，要用一个长的像正态函数的函数取近似，这样的函数服从$latex N(x_0, 1/f''(x_0))$.
下面举个例子来计算
$$\int_{-\infty}^{\infty} x^2 e^{-x^2/2} \mathrm{d} x $$.
这个积分的结果是$latex \sqrt{2\pi}$，这可以这样计算出来。
假设$latex Z$是一个标准正态分布，那么：
$$\int_{-\infty}^{\infty} x^2 e^{-x^2/2} \mathrm{d} x = \sqrt{2\pi} E(Z^2) = \sqrt{2\pi} Var(Z) = \sqrt{2\pi} = 2.507$$.
用拉普拉斯方法：
$$\int_{-\infty}^{\infty} x^2 e^{-x^2/2} \mathrm{d} x = \int_{-\infty}^{\infty} e^{-x^2/2 + 2 \log{x}} \mathrm{d} x $$.
对$latex f(x)$求导：
$$
\begin{align}
f(x) &= -\frac{x^2}{2} + 2 \log{x} \\
f'(x) &= -x + \frac{2}{x} \\
f''(x) &= -1 - \frac{2}{x^2}
\end{align}
$$
令$latex f'(x) = 0$，可以解出$latex x_0 = \sqrt{2}$.
我们有$latex f(x_0) = -1 + \log{2}$ 和 $latex f''(x_0) = -2$.
积分结果为：
$$
e^{f(x_0)} \sqrt{\frac{2\pi}{|f''(x_0)|}} =
e^{-1 + \log{2}} * \sqrt{\frac{2\pi}{|-2|}} = \frac{2}{e} \sqrt{\pi} = 1.304
$$
比较2.507 和1.304，我们发现理论结果和拉普拉斯方法的结果几乎差了一倍。
为啥差别那么大呢？
看下面的图：
[caption id="attachment_564" align="alignnone" width="300"]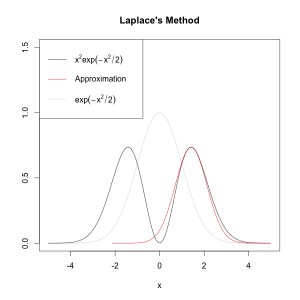
Demo Laplace Method[/caption]
我们发现要求的积分值是黑色曲线下的面积。拉普拉斯方法想用灰色曲线（$latex e^{-\frac{x^2}{2}}$）通过拉伸得到红色曲线，然后用红色曲线下的面积来近似积分。但是由于黑色曲线有两个峰值，这个近似显然不算成功。
所以拉普拉斯方法是有局限性的：被积分的函数有一个峰值，并且和正态曲线长的像。这种情况下的近似才能比较精确。
对于概率密度函数，（无论一维还是多维），大部分都是一个峰值。或者因为中心极限定理，统计量均值的分布和正态函数很像，也是一个峰值。因此拉普拉斯方法的用处还是很多的。此外，拉普拉斯方法计算很快。比如在线性混合效果模型中，拉普拉斯方法是用的最广的方法，也可能是唯一能在实际中使用的方法［2-4］。
［1］维基百科 http://en.wikipedia.org/wiki/Laplace’s_method
［2］Approximate Inference in Generalized Linear Mixed Models. N. E. Breslow and D. G. Clayton. Journal of the American Statistical Association Vol. 88, No. 421 (Mar., 1993) , pp. 9-25
［3］Variance component testing in generalised linear models with random effects. XIHONG LIN. Biometrika (1997) 84 (2): 309-326.
［4］lme4 package Douglas Bates et al. http://cran.r-project.org/web/packages/lme4/lme4.pdf (see nAGQ parameter)