利用矩阵的分解和分析图是个很有意思的话题。当我们能用这个技术来改进PCA的时候,或者降维的时候,我们有可能相信有意思的结果会蹦出来。这里主要参考了文献【1】和Pluskid的blog【2】。其中【1】给出了推导过程:目标函数是二次型的矩阵,约束同样是二次型的;还有详细的Algorithm:里面最关键的一步是Generalized eigenvector problem(wiki有非常简短的介绍),理论上可以用Golub Matrix Computation Chapter 8 的方法(我没读,差不多忘了Numerial Method课的知识了),但我并没有使用。另外【2】里的文字流畅,言简意赅,是入门的好文章。
简单来讲,当利用k-neighbor 或\( \epsilon \)方法构造临街矩阵,利用Simpled minded(0 or 1)或者Heat Kernel来构建Weight矩阵后,我们的问题是求解:
$$ L f = \lambda D f \quad st. \quad f^T D f = 1 \quad \mathrm{and} \quad f^T D \mathbf{1} = 0 $$
我们已经知道D是一个对角阵,所以求解$$ D^{-1} L f = \lambda f $$即可。
考虑到约束条件,我们只需对每一个\(f[\latex]做如下变换:
$$ f^T D f = 1 \Rightarrow f = f / \sqrt{\sum_i f_i^2 d_i} $$
$$ f^T D \mathbf{1} = 0 \Rightarrow f = f – \frac{ \sum_i f_i d_i } { \sum_i d_i} $$
R code
LaplacianEigenmap.R Link
LaplacianEigenmapTest.R Link
结果:
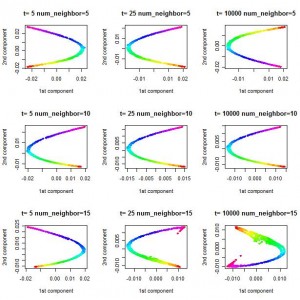
从 [latex] 0 = \lambda_0 \le \lambda_1 \le \lambda_2 \ldots \lambda_n \) 中取最小的两个非零的特征根\( \lambda_1\, \lambda_2 \)对应的特征向量,仿照paper,得到结果如下:
注意,这里的图案和paper不符,但我的验算,检查是否是特征值、约束条件,表明我的计算过程应该是正确的。
另外Pluskid 的Blog上的图案中,Laplacian Eigenmap的结果是一个彩带, 我认为有可能是使用了\( \lambda_0, \lambda_1 \)对应的特征向量。
参考:
【1】Mikhail Belkin and Partha Niyogi, “Laplacian Eigenmaps for Dimensionality Reduction and Data Representation,” Neural Computation 15, no. 6 (February 6, 2011): 1373-1396.
【2】漫谈 Clustering (番外篇): Dimensionality Reduction http://blog.pluskid.org/?p=290